ウサギとカメの成果競争

題名：ウサギとカメの成果競争
報告者：ナンカイン

　ウサギとカメと言えば、即座に思い出すのが、「ウサギとカメ」の話である。作者はイソップ(ギリシアの伝説的な寓話作家で、ギリシア名はアイソポス(Aisōpos)1))とされる。イソップが亡くなったのは、紀元前564年頃であるが1)、そのはるか昔の作家による話が今でも読まれている理由として、そのイソップによる話には、人間社会における普遍的な事実が隠されていることに他ならない。「ウサギとカメ」もその通りである。話の大筋は、「ウサギとカメが競走することになりました。はしりはじめてしばらくするとウサギはうしろがきになりふりかえってみました。カメのすがたはまったくみえません。「あ、にんじんだ。おいしそう」。ウサギはにんじんばたけで寝てしまいます。するとカメが…」2)である。最終的には、油断した(自分の力を過信した)ウサギは、(地道に努力した)カメに屈する、ことになっている。
　一方、その話の分かりやすさゆえに、数学(算数)的にも問題化されることが少なくない。例えば、ウサギとカメの歩行速度を提示し、ゴールまでの距離を提示した場合に求めるウサギの睡眠時間3)や、ウサギの睡眠時間を提示した場合に求めるゴールまでの距離4)などが、その問題に相当する。
　ここで、問題としたいのが、ゴールまでの距離である。ウサギとカメの競争では、ゴールまでの距離は約2 kmほどである3, 4)。しかしながら、このゴールを単純な距離ではなく、ある目標に対するゴールと捉え直すと、そこには、kmでは表せない概念、時間が必要となる。あるいは、それを日、年と置き換えても構わない。例えば、あるプロジェクトが進行したとする。それに対して、1年後には何らかの成果を出さないといけないと仮定する。すると、どのくらいのペースで、そのプロジェクトに関わる目的を進行しないといけないかという問題は、基本的にウサギとカメと同じ内容である。しかしながら、計算上ではやや数式化しにくい。そこで、単純に考え、最大の成果を達成したら10として、各月ごとのプロジェクトの進行度合いを見ると、図のような一例ができる。



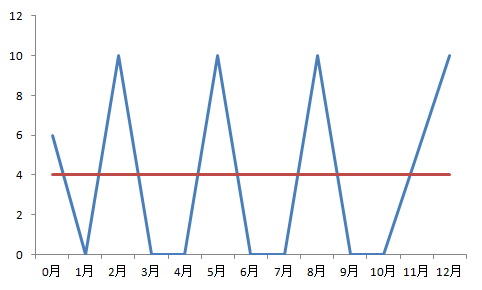
図　あるプロジェクトの成果

青線はAさんの方法、赤線はBさんの方法で、横軸が月齢、縦軸が成果とする。一見すると、Aさんすごいな、と思える。しかしながら、最終的な平均はAさん3.9成果、Bさん4.0成果となり、Bさんの方が優秀となる。たぶん、Aさんは12月にはへとへとであろう。もしかすると、体を壊したかもしれない。それに比べて、常に一定のBさんは、少なくとも体への負担は少ない。これを言い換えると、最高速度を求めるよりも、持続した平均速度を求める方が、成果としては無理なく得られやすいことがよく分かる5)。カメはこのBさんに相当する。

1) https://kotobank.jp/word/イソップ-31036 (閲覧2016.3.24)
2) http://www.amazon.co.jp/ウサギとカメ-イソップえほん4-蜂飼-耳/dp/4265066941 (閲覧2016.3.24)
3) http://web.kusokagaku.co.jp/articles/163 (閲覧2016.3.24)
4) http://www.e-juken.jp/blog/maeda/2011/05/4.html (閲覧2016.3.24)
5) http://www.lifehacker.jp/2016/03/160323habit_graduation.html (閲覧2016.3.24)

From ここから。© 2015 This is 地底たる謎の研究室 version。