題名:ピタゴラスの定理への理解
報告者:ログ
例えば、街中を歩くと、ふと地面には綺麗なタイルが並んでいることがある。これを正方形のタイルとする。さらに、その正方形のタイルには対角線となる位置に線が入っている。そのタイルを巧妙に4枚づつ組み合わせて並べられているのであれば、その4枚から内側にひし形が誕生することがある。それが図1となる。このタイルの組み合わせの並び方において、タイル一枚の辺の長さをa、対角線の長さをcとすると、そこに定理が現れる。
4 × (1/2 × a2) = c2
である。この式の左辺はタイルの外側に位置する三角形の4つ分の面積を示し、右辺は対角線で囲まれた正方形の面積を示す。この式から、タイルの辺がなす面積と対角線がなす面積との関係が導かれる1)。ただし、このタイルは正方形の完全なタイルの並びの場合となる。
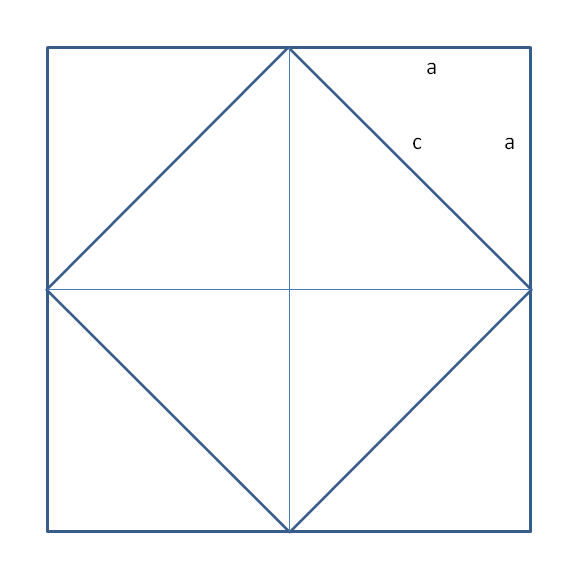
図1 完全なタイルの並び
次は、このタイルが製造過程で正方形でなくなり、長方形形となってしまった不完全なタイルの場合を考えてみる。このようなタイルでもタイル業者やタイル貼り施工業者にこだわりがなければ、「不完全なタイルでも貼ってしまえ」、となるかもしれない。すると、不完全なタイルにおける並び方は、タイルが正方形でなく、長方形であることから、図2のように中央に正方形の穴ができてしまう。これで、図1の場合と同様に定理を求めるとなると、タイルの辺の4つ分の面積は対角線の面積の一部で、この4つ分の面積に中央の正方形の面積を足すと、対角線がなす面積となることが理解できる。すなわち、
4 × (1/2 × ab) + (b-a)2 = c2
で表され、これをまとめると、以下の式が導かれる。これは
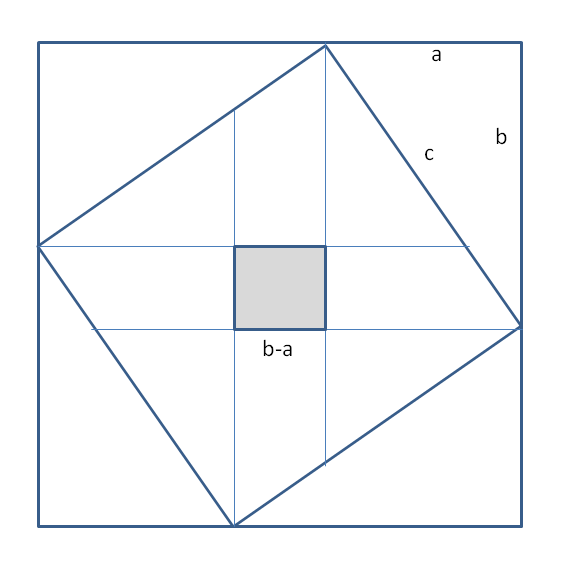
図2 不完全なタイルの並び方
まさに、ピタゴラスの定理に他ならない。
a2 + b2 = c2
1) http://blog.donaldo-plan.com/archives/2915 (閲覧2017.6.16)
From ここから。© 2015 This is 地底たる謎の研究室 version。
ピタゴラスの定理への理解
「宇宙コロニー( Off-world colonies )での新しい生活が貴方を待っています。チャンスと冒険に満ちた黄金の土地に、再び巡ってきた好運。」 “A new life awaits you in the Off-world colonies. The chance to begin again in a golden land of opportunity and adventure.”

