題名:スキーにおけるスピードを計算する
報告者:ログ
ウィンタースポーツの代表と言えば、スキー(スノボ)とスケートになるであろう。スキー(スノボ)は屋外がメインとなり、スケートは室内がメインとなる。そのため、屋外の天候にも左右されやすいが、雪質がよく、かつ、天気も良い日のスキー(スノボ)は、まさしく「ウィンターなスポーツしているなぁ」という感じである。
かつて「私をスキーに連れてって」という映画の影響もあってか、その当時のスキー場はとても活性化していた。しかしながら、現在はスキー(スノボ)をする人口が当時よりも減少し、昨今のスキー場は、かつてほどの盛況がないこともしばしばである。軒並み、スキー場も合併や閉鎖も与儀なくされている。スキー(スノボ)の最大の欠点は、どうしても冬の気候の影響が無視できないこともあり、これは地球の温暖化の影響もあろうが、やはり雪がなければ、スポーツ以前にスキー場が営業できない。人工の雪による施設も散見されるも、自然の雪一面に覆われた山の斜面での爽快な気分は、他のスポーツには得られない優越感である。ゆえに、これがスキー(スノボ)のスポーツとしての最大の利点でもある。
スキー(スノボ)をやり始める、あるいは、スキー(スノボ)が上達すると、気になるのはそのスピードである。むろん、カーブを如何にして曲がるか、あるいは、ジャンプを如何にしてこなすかも、その上達に応じて必要となる知識であるが、まず始めに気になる知識はスピードである。そこで、ここでは、スキー(スノボ)に伴うスピードについて計算したい。
まず計算を簡単にするために仮定として、スキー(スノボ)をする斜面は一定の傾きΘの斜面で、スキー板(スノボ板)にはワックスが丁寧に塗られて摩擦はほぼ0とする。また、スキーヤー(スノーボーダー)の空気抵抗はないものとする。さらに、スキーヤー(スノーボーダー)の体重(質量)をmとして、重力加速度をgとする。図からスキーヤー(スノーボーダー)の斜面への力はmgsinΘとなり、加速度はgsinΘとなる。スタートからゴールまでの斜面の距離をxとして、スキーヤー(スノーボーダー)のゴール地点の速度をvとすると、v2 = 2gsinΘx → v = sqrt(2gsinΘx)でゴール地点のスピードが計算できる。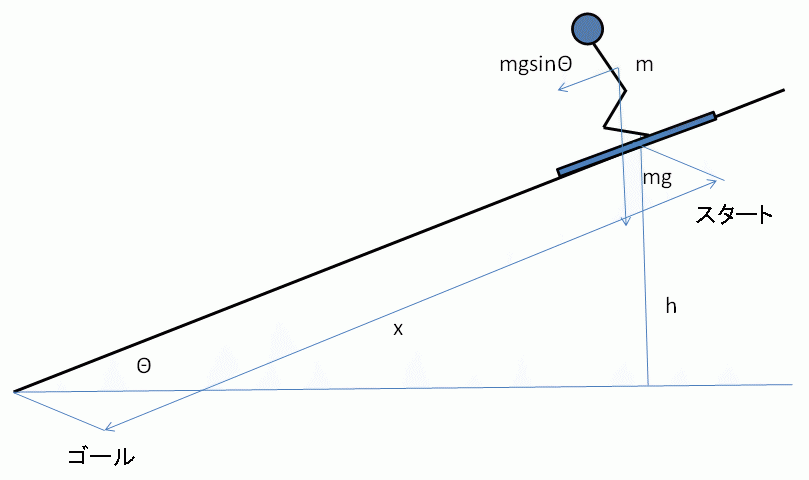
図 スキーヤー(スノーボーダー)のスピード
斜面の高さhが分かれば、位置エネルギーと運動エネルギーより、v = sqrt(2gh)となる(xsinΘ = hからの代入でも計算可)。このことから、スキーヤー(スノーボーダー)の体重(質量)に関係なく、ゴール地点での速度が決定される。しかしながら、文献1)にもあるように、空気抵抗の影響は無視できず、スキーヤー(スノーボーダー)の体重(質量)が重いほど、空気抵抗の力による最終スピードは大きくなる。すなわち、重いほど最高スピードが速いことになる。一方、文献2)にもあるように、単純にすべり降りるだけなら、スキーヤー(スノーボーダー)の体重(質量)が重いほうが、空気抵抗の影響が小さくなる分、有利であるが、カーブでは強力な遠心力に抵抗する必要があり、これはスキーヤー(スノーボーダー)の体重(質量)が重いほど不利になる。逆に言えば、スキーヤー(スノーボーダー)の体重(質量)が軽いほうが、より早いスピードでカーブを曲がれることとなる。これが、仮定でない実践のスキー(スノボ)では、難しい…。
1) http://www.ayim.net/blog/?p=5462 (閲覧2017.3.13)
2) https://oshiete.goo.ne.jp/qa/460606.html (閲覧2017.3.13)
From ここから。© 2015 This is 地底たる謎の研究室 version。

