題名:ハムスターの回し車における発電量の計算
報告者:ダレナン
これまで当ブログではハムスターに関する様々な研究を報告した。ここでは、この記事でも記載したハムスターの回し車(ハムスターの仕事)に関して、物理学的な意味での仕事率を求め、ハムスターの回し車における発電量について検討したい。なお、ねずみの発電量に関しては、橋本英文博士の文献1)に先行研究がある。そこで、ここでは、博士の研究に基づいて、それをハムスターの回し車に置き換えることで検討したい。
橋本博士によれば、輪(回し車に相当)を10秒に6回の割合で回転させているとして、輪の半径rが8cm、輪の質量Mが50g、ねずみの質量mを50gとして、ねずみの平均荷重位置を輪の中心角で底から45度の周上との仮定で計算している(図)。
まず輪のvは、輪の周の長さ×6回分/10秒で求められるため、
v = 2πr×6/10 = 2×3.14×0.08×6/10 = 0.301m/s
となる。ねずみが輪にした回転の運動エネルギーKとすると、
K = Mv2/2 = 0.05×(0.301)2/2 = 0.00225Nm
となる。さらに、輪を回す位置のねずみの分力Fは
F = mg×cos45°= 0.05×9.8×0.707 = 0.346N
で求められるために、仕事率Pは
P = Fv = 0.346×0.301 = 0.104Nm/s = 0.104W
となる。
次にこれらの計算をハムスターで置き換える。ハムスターの研究レポート2)によると、ハムスターは回し車で、一日に平均12.90km、平均速度2.73km/hの仕事をする。このレポートでは、ゴールデンハムスターで実施しているが、回し車の詳細が不明であったために、回し車の設定や、回し車を回すハムスターの位置については橋本博士に準ずる。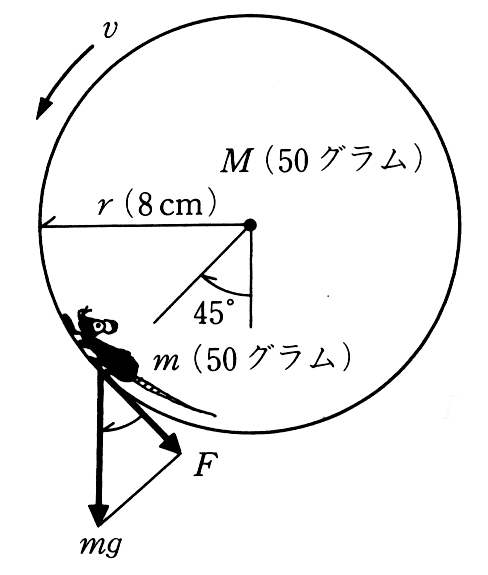
図 ねずみでの条件1)
なお、レポートにはゴールデンハムスターの正確な体重(質量)の記載もなかったが、100~200gと記載されていたために、ここではmを150gと仮定する。
2.73km/hは0.758m/sであることから、ハムスターの回転の運動エネルギーは、
K = 0.05×(0.758)2/2 = 0.01436Nm
となる。ハムスターの分力Fは
F = 0.15×9.8×0.707 = 1.039N
となり、仕事率Pは
P = Fv = 1.039×0.758 = 0.787W
となり、先のねずみと比較すると、約7.56倍の発電量があることが計算された。しかしながら、レポートはゴールデンハムスターで実施しているために、発電量も大きくなったことが推測され、これよりも小型のジャンガリアンやロボロフスキー、キャンベルなどになると、もっと発電量が少ないかもしれない。
1) 橋本英文: おもしろ力学. コロナ社. 1993.
2) http://www.pro--f.com/my/ham_rpt.pdf (閲覧2017.5.25)
From ここから。© 2015 This is 地底たる謎の研究室 version。

