人生はドーナツなのだ

題名：人生はドーナツなのだ
報告者：ダレナン

　本記事は、この記事の続きです。

　先の記事にて、数学におけるトポロジー(位相幾何学)を学んだ。その学び方は、まさに先の記事で示したモデルのアナベル明さんと同じく、かじったドーナツの程度でしかないかもしれない。そのため、ここでも筆者の浅学非才を暴露するようなものでもあるが、千里の道も一歩からである。そして、そこでもって、人生はドーナツへと至るのかもしれない。これを、天才バカボン風に言えば、「人生はドーナツなのだ」となる。
　ここで、ここでの記事を復習してみたい。おもちゃのスリンキーを丸くつなげる形状へと発展させると、スリンキーの連続体が生まれる。そのスリンキーの連続体の大きな輪の中央には、ドーナツの穴に相当する中空の空間があり、個々の輪の中にもチューブのような中空の空間が存在する。そこで、ドーナツをスリンキーの連続体へと発展させる方法として捉えると、次のように考えることができる。

「トーラス(ドーナツ)上のホモローグ0(*)でない切断線Z1でもって、Z⊕Z={(n, 0)}(nはスリンキーの個々の輪の数、ここでの記事では51)という1次元ホモロジー群が1)、ドーナツとスリンキーの連続体にある関係」

と見なすことができる(かもしれない)。そうして、切断線Z1でもって展開されたスリンキーの連続体は、厚みや幅はないが大きなドーナツとなるも、トーラスΣ1であることには変化はない。
　この個々の輪を1年での人生の時点とすると、大きな輪は人生の始めから終わり、すなわち、生から死となる。その個々の輪の数、先ほどの説明で言えば、nは人によって異なるが、最終的にはドーナツ(トーラス)として人生が巡る。
　スリンキーの連続体の中空の空間、あるいは、トーラスΣ1(ドーナツ)の内部は、こちらの記事でも示したように、「超越性の領域」であり、トーラスΣ1(ドーナツ) に閉曲線を引き、この曲線に2つの点P, Qをとっても、閉曲線の両側は両側に見えて、実は両側ではなく、外側でもなく1)、内側でもない「超越性の領域」となる。



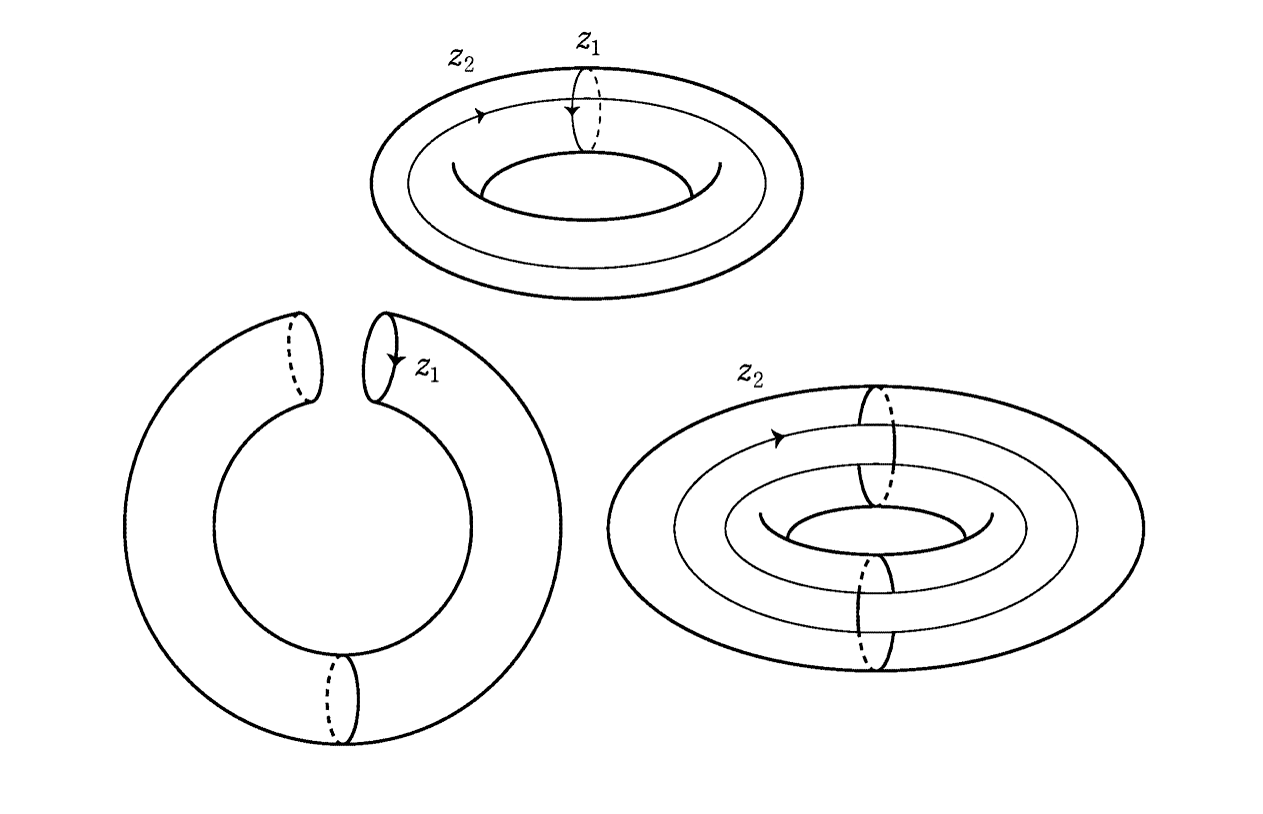
図　トーラス(ドーナツ)の切断線1)

ただし、厚みや幅はないが大きなトーラスΣ1(ドーナツ)を閉曲線として見ると、そこには、2つの点P, Qをとると、両側は両側となり、内と外が生まれる。これがこちらの記事で示した生と死の境界として観察されている現象となる (かもしれない)。そうして、果てしないトポロジーへの知識欲は、依然として境界が見えない永遠の学びの連結性を、ここで持ち始める。傾愛してやまないトポロジーの始祖でもある天才数学者レオンハルト・オイラー博士の、せめてハナクソにでも…なりたいと願う。

*: ホモローグ0：定義：曲面M上の閉曲線を曲面上の切断線といい、その切断線が曲面を2つの部分に分けるとき、その閉曲線をホモローグ0という1)。ちなみに、トーラス(ドーナツ)では2つの切断線Z1、Z2で切断しても球面と異なり、曲面は2つに分割されない(図)。
1) 瀬山士郎: はじめてのトポロジー. PHP研究所. 2014.

From ここから。© 2015 This is 地底たる謎の研究室 version。